Аркфункции
Арксинус
y = arcsin x
Является обратной для y = sin x
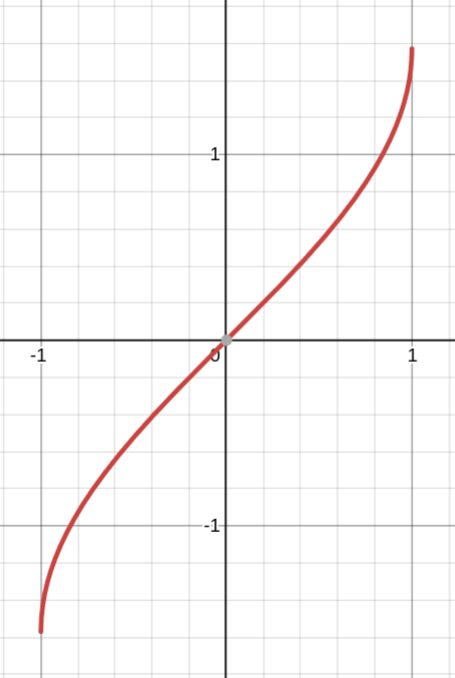
Свойства:
1. Область определения: D(y) = [−1; 1]
2. Область значений: E(y) = [−π/2; π/2]
3. Функция нечётная (arcsin(−x) = −arcsin x)
4. Точки пересечения с осями координат: (0; 0)
5. Промежутки знакопостоянства:
arcsin x < 0 при x ∈ [−1; 0)
arcsin x > 0 при x ∈ (0; 1]
6. Промежутки возрастания и убывания:
возрастает на промежутке x ∈ [−1; 1]
Арккосинус
y = arccos x
Является обратной для y = cos x
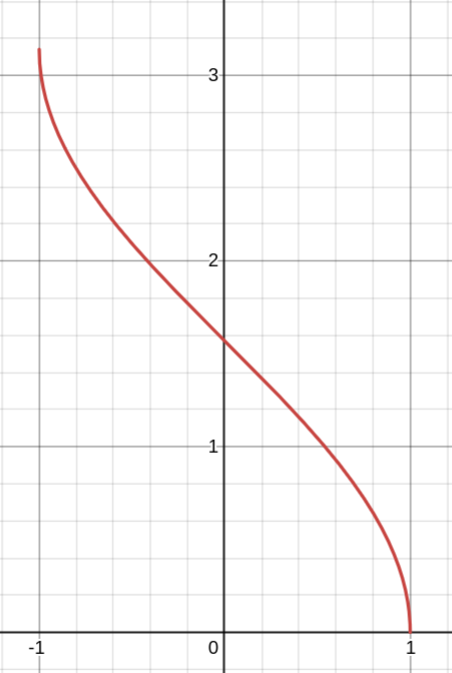
Свойства:
1. Область определения: D(y) = [−1; 1]
2. Область значений: E(y) = [0; π]
3. Функция ни чётная, ни нечётная
4. Точки пересечения с осями координат: с Ox: (1; 0); с Oy: (0; π/2)
5. Промежутки знакопостоянства:
arccos x > 0 при x ∈ [−1; 1)
6. Промежутки возрастания и убывания:
убывает на промежутке x ∈ [−1; 1]
Арктангенс
y = arctg x
Является обратной для y = tg x
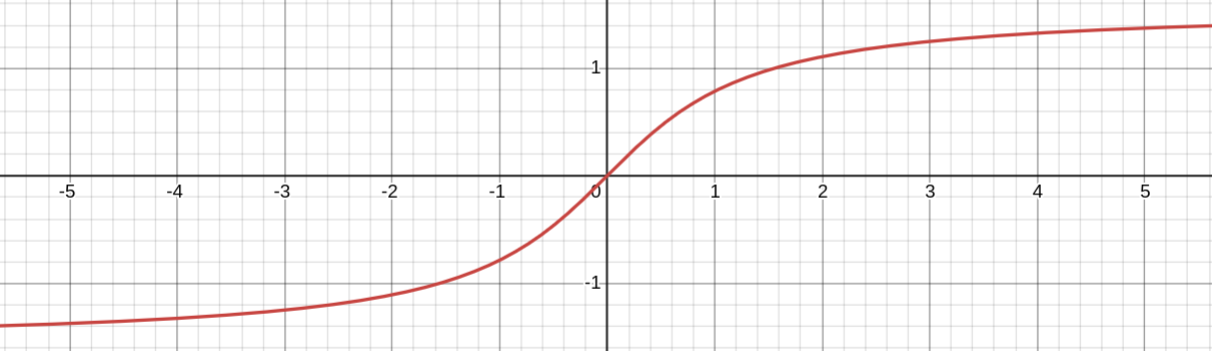
Свойства:
1. Область определения: D(y) = R
2. Область значений: E(y) = (−π/2; π/2)
3. Функция нечётная (arctg(−x) = −arctg x)
4. Точки пересечения с осями координат: (0; 0)
5. Промежутки знакопостоянства:
arctg x < 0 при x ∈ (−∞; 0)
arctg x > 0 при x ∈ (0; +∞)
6. Промежутки возрастания и убывания:
возрастает на промежутке x ∈ (−∞; +∞)
Арккотангенс
y = arcctg x
Является обратной для y = ctg x
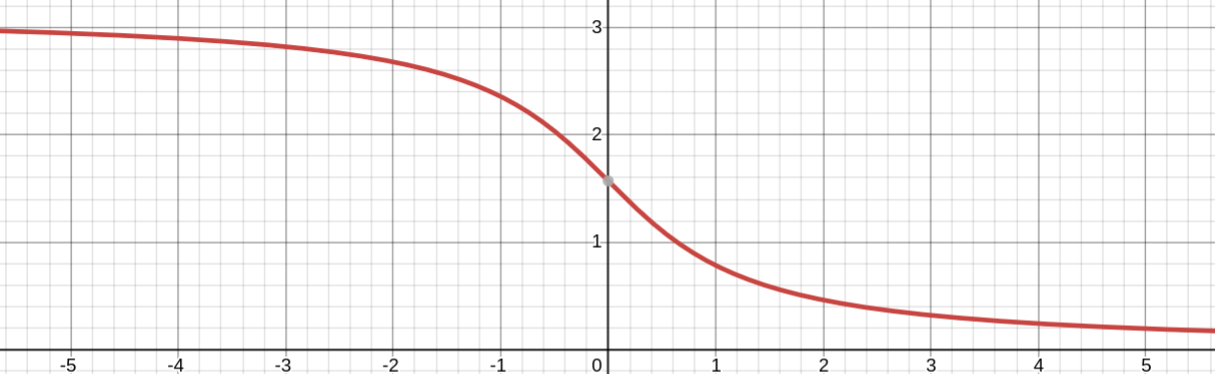
Свойства:
1. Область определения: D(y) = R
2. Область значений: E(y) = (0; π)
3. Функция ни чётная, ни нечётная
4. Точки пересечения с осями координат: Oy: (0; π/2)
5. Промежутки знакопостоянства:
arcctg x > 0 при x ∈ (−∞; +∞)
6. Промежутки возрастания и убывания:
убывает на промежутке x ∈ (−∞; +∞)
Арксеканс
y = arcsec x
Является обратной для y = sec x
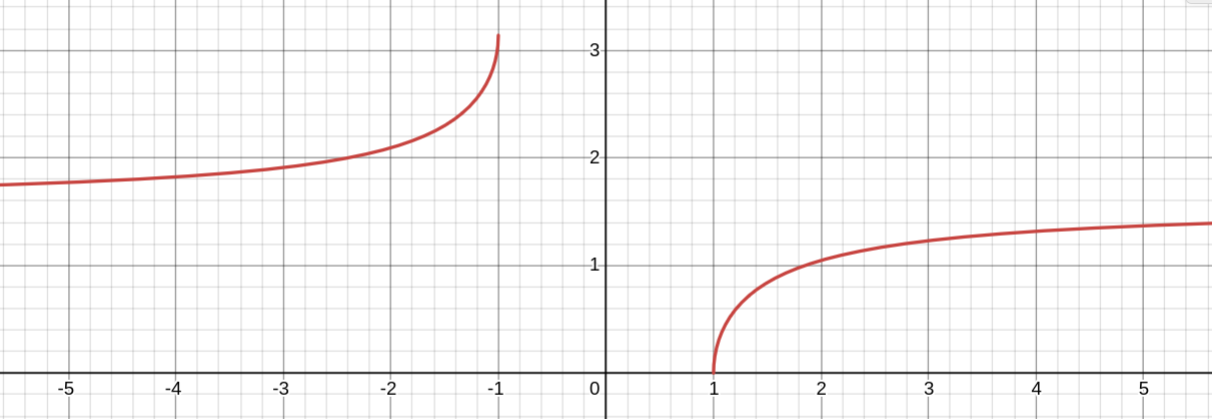
Свойства:
1. Область определения: D(y) = (−∞; −1] ∪ [1; +∞)
2. Область значений: E(y) = [0; π/2) ∪ (π/2; π]
3. Функция ни чётная, ни нечётная
4. Точки пересечения с осями координат: Ox: (1; 0)
5. Промежутки знакопостоянства:
arcsec x > 0 при x ∈ (−∞; −1] ∪ (1; +∞)
6. Промежутки возрастания и убывания:
возрастает на промежутке x ∈ (−∞; −1] ∪ [1; +∞)
Арккосеканс
y = arccosec x
Является обратной для y = cosec x
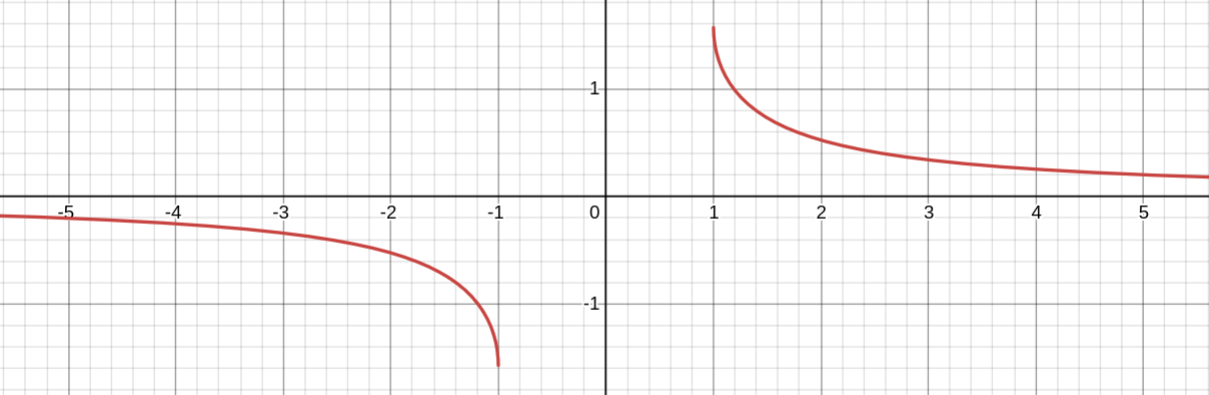
Свойства:
1. Область определения: D(y) = (−∞; −1] ∪ [1; +∞)
2. Область значений: E(y) = [−π/2; 0) ∪ (0; π/2]
3. Функция нечётная (arccosec(−x) = −arccosec x)
4. Точки пересечения с осями координат: отсутствуют
5. Промежутки знакопостоянства:
arccosec x < 0 при x ∈ (−∞; −1]
arccosec x > 0 при x ∈ [1; +∞)
6. Промежутки возрастания и убывания:
убывает на промежутке x ∈ (−∞; −1] ∪ [1; +∞)